The concept of Fibonacci Sequence or Fibonacci Number is widely used in many programming books.
It could be defined via the formula:
F(0)=1,F(1)=1, F(n)=F(n-1)+F(n-2)
In ES6 there is a feature so called “generatorFunction” which can achieve the calculation of Fibonacci Sequence in a very convenient way. But before we really enjoy the built-in language feature, let’s first see how to simulate it in ES5.
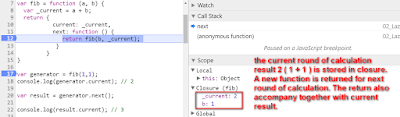
Here I use the closure in JavaScript to store the current round of calculation and return a new function for next round trigger.
var fib = function (a, b) {
var _current = a + b;
return {
current: _current,
next: function () {
return fib(b, _current);
}
}
}
var generator = fib(1,1);
console.log(generator.current); // will print out 2
var result = generator.next();
console.log(result.current); // will print out 3
It could be defined via the formula:
F(0)=1,F(1)=1, F(n)=F(n-1)+F(n-2)
In ES5
In ES6 there is a feature so called “generatorFunction” which can achieve the calculation of Fibonacci Sequence in a very convenient way. But before we really enjoy the built-in language feature, let’s first see how to simulate it in ES5.
Here I use the closure in JavaScript to store the current round of calculation and return a new function for next round trigger.
var fib = function (a, b) {
var _current = a + b;
return {
current: _current,
next: function () {
return fib(b, _current);
}
}
}
var generator = fib(1,1);
console.log(generator.current); // will print out 2
var result = generator.next();
console.log(result.current); // will print out 3
Suppose I would like to get a series of result and I am too lazy to call next again and again, then I write a tool function to ease my life:
var take = function(n, sequence) {
var result = [];
var temp = sequence;
for (var i = 0; i < n; i++) {
result.push(temp.current);
temp = temp.next();
}
return result;
}
Then I can get 10 rounds of calculation result via a single shot:
console.log(take(10, fib(1,1)));
Result in console:
In ES6
Now we have generatorFunction which makes life pretty easier.
The complete source code:
var fib_generator = function *(){
var current = 0, next = 1;
while(true)
{
[next, current] = [next+current, next];
yield current;
}
}
var fib = fib_generator();
for(var i = 0; i < 10; i++)
{
console.log(fib.next().value);
}
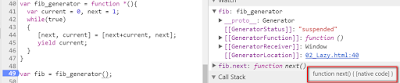
How does this native function generator work
In line 40~47 we get a function generator with ES6 grammar function *().
Within the body we declare an endless loop to calculate Fibonacci sequence.
In line 49 we call this generator via () and store its result via variable fib. Here the code in line 41~45 is never executed so far.
Instead, the variable fib just holds a ITERATOR reference to function generator fib_generator.
This ITERATOR has a built-in method next supported by ES6. When this next method is called ONCE, the body in fib_generator is then executed ONCE as well.
Now let’s step into next call for the first time:
Pay attention to the callstack change:
Once yield is executed, the current iteration result is returned from function generator to consumer:
Change the consumer code a little bit to make result returned by yield more clearly understood:
for(var i = 0; i < 10; i++)
{
var currentResult = fib.next();
console.log(currentResult.value);
}
Now it is clear that yield keyword returns an object with one attribute which stores current calculated result, and a boolean done flag to indicate whether the function generator has ended. In my case it is always false which makes sense since I declare a while(true) inside it.
Final result:
In ABAP
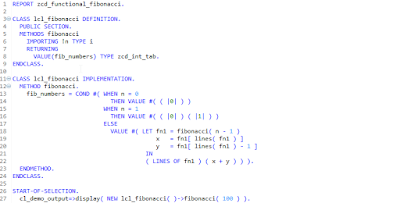
In this simple report ( written by my colleague Lin Xun ), two different calculation approaches are demonstrated:
REPORT Z_FIBO.
PARAMETERS: N type i,
v1 RADIOBUTTON GROUP v default 'X',
v2 RADIOBUTTON GROUP v.
data: f type i,
t type i.
data: product_guid type comm_product-product_guid.
get run time field t.
case 'X'.
when v1. perform fibonacci using n changing f.
when v2. perform fibonacci_2 using n changing f.
endcase.
write: / 'Fibonacci(', n, ') =', f.
get run time field t.
write: / 'Runtime', t, 'microseconds'.
*&---------------------------------------------------------------------*
*& Form fibonacci
*&---------------------------------------------------------------------*
form fibonacci using in type i
changing fib type i.
data: f_1 type i, f_2 type i,
n_1 type i, n_2 type i.
case in.
when 0. fib = 1.
when 1. fib = 1.
when others.
n_1 = in - 1.
n_2 = in - 2.
perform fibonacci using n_1 changing f_1.
perform fibonacci using n_2 changing f_2.
fib = f_1 + f_2.
endcase.
endform. "fibonacci
*&---------------------------------------------------------------------*
*& Form fibonacci_2
*&---------------------------------------------------------------------*
form fibonacci_2 using in type i
changing fib type i.
data: f_1 type i, f_2 type i,
n_1 type i, n_2 type i,
l type i.
data: fibo type table of i.
append 1 to fibo. " fibonacci(0)
append 1 to fibo. " fibonacci(1)
n_1 = 1.
n_2 = 2.
l = in - 1.
do l times.
read table fibo index n_1 into f_1.
read table fibo index n_2 into f_2.
fib = f_1 + f_2.
add 1 to n_1. add 1 to n_2.
append fib to fibo.
enddo.
endform. "fibonacci_2
Execute report you can find out that the second approach to calculate using ABAP internal table is greatly faster than the first solution.
The approach to simulate next call is also very simple:
CLASS zcl_fibo DEFINITION
PUBLIC
FINAL
CREATE PUBLIC .
PUBLIC SECTION.
CLASS-METHODS next
RETURNING
VALUE(rv_result) TYPE int4 .
PROTECTED SECTION.
PRIVATE SECTION.
CLASS-DATA sv_current TYPE int4 VALUE 0 ##NO_TEXT.
CLASS-DATA sv_next TYPE int4 VALUE 1 ##NO_TEXT.
ENDCLASS.
CLASS ZCL_FIBO IMPLEMENTATION.
METHOD next.
rv_result = sv_next + sv_current.
sv_current = sv_next.
sv_next = rv_result.
ENDMETHOD.
ENDCLASS.
Consumer code:
REPORT ZFIBO.
DO 10 TIMES.
WRITE: / zcl_fibo=>next( ).
ENDDO.
Output:








No comments:
Post a Comment